Sebelumnya sudah dibahas algoritma konversi bilangan desimal dan biner. Kemudian dibahas bahasa pemrograman pascal. Nah, apa hubungan nya kedua materi ini? Mari kita lihat pengertian algoritma yang diambil dari Wikipedia.
Sudah paham apa hubungan algoritma dengan bahasa pemrograman pascal? Jika belum, mari kita bandingkan program konversi bilangan desimal ke biner yang ditulis dengan bahasa pascal, dengan algoritma nya.
Sudah ketemu apa hubungan nya algoritma dengan program pascal? Jadi, algoritma itu langkah-langkah membuat program nya. Nanti nya langkah-langkah itu yang diterjemahkan dengan bahasa pascal sehingga menjadi bahasa pascal yang bisa dijalankan.
Jika mau lancar membuat program pascal sebaiknya harus paham bagaimana cara menyusun algoritma yang tepat, sehingga akan lebih lancar dalam menyusun program pascal.
Sistem bilangan biner atau sistem bilangan basis dua adalah sebuah sistem penulisan angka dengan menggunakan dua simbol yaitu 0 dan 1. Sistem bilangan biner modern ditemukan oleh Gottfried Wilhelm Leibniz pada abad ke-17. Sistem bilangan ini merupakan dasar dari semua sistem bilangan berbasis digital. Dari sistem biner, kita dapat mengkonversinya ke sistem bilangan Oktal atau Hexadesimal. Sistem ini juga dapat kita sebut dengan istilah bit, atau Binary Digit. Pengelompokan biner dalam komputer selalu berjumlah 8, dengan istilah 1 Byte/bita. Dalam istilah komputer, 1 Byte = 8 bit. Kode-kode rancang bangun komputer, seperti ASCII, American Standard Code for Information Interchange menggunakan sistem peng-kode-an 1 Byte.
Perhitungan
Perhitungan dalam biner mirip dengan menghitung dalam sistem bilangan lain. Dimulai dengan angka pertama, dan angka selanjutnya. Dalam sistem bilangan desimal, perhitungan mnggunakan angka 0 hingga 9, sedangkan dalam biner hanya menggunakan angka 0 dan 1.
- Sebuah panah langsung mengacu pada penghubung dari ayah ke anak nya (panah di gambar dalam pohon).
- Akar dari pohon adalah simpul tanpa ayah. Terdapat paling banyak satu akar dalam pohon berakar.
- Sebuah daun adalah simpul yang tidak memiliki anak.
- Kedalaman sebuah simpul n adalah panjang jalan dari akar ke simpul. Himpunan semua simpul pada kedalaman yang diberikan kadang-kadang dinamai dengan Tingkat (Level) dari pohon. Akar memiliki kedalaman kosong.
- Tinggi sebuah pohon adalah panjang jalan dari akar ke daun-daunnya.
- Saudara adalah simpul yang memiliki ayah yang sama
- Jika terdapat sebuah jalan dari simpul p ke simpul q, dimana simpul p lebih dekat ke akar daripada q, maka p adalah leluhur dari q dan q adalah keturunan p.
- Lebar daris sebuah simpul adalah jumlah keturunan termasuk simpul itu sendiri.
Jenis pohon biner
- Sebuah pohon biner berakar (rooted binary tree) adalah sebuah pohon berakar dimana setiap simpul paling banyak mempunyai dua anak
- Sebuah pohon biner penuh (full binary tree), atau pohon biner asli (proper binary tree), adalah sebuah pohon dimana setiap simpul mempunyai nol atau dua anak.
- Sebuah pohon biner sempurna (perfect binary tree) (atau kadang-kadang pohon biner lengkap (complete binary tree) adalah sebuah pohon biner penuh dimana semua daun memiliki kedalaman yang sama.
- Sebuah pohon biner lengkap (complete binary tree) dapat didefinisikan juga sebagai sebuah pohon biner penuh dimana semua daunnya memiliki kedalaman n atau n-1 untuk beberapa n. Agar sebuah pohon dapat menjadi sebuah pohon biner lengkap, semua anak pada tingkat terakhir harus menempati titik terkiri secara teratur, dengan tidak ada titik yang menganggur di antara keduanya. Sebagai contoh, jika dua simpul pada tingkat terbawah masing-masing menempati sebuah titik dengan suatu titik kosong di antara keduanya, tetapi sisa simpul anaknya terhimpit tanpa titik di antaranya, maka pohon tersebut tidak dapat membentuk sebuah pohon biner lengkap karena titik kosong tersebut.
- Sebuah pohon biner lengkap berakar (rooted complete binary tree) dapat dikenali dengan magma bebas.
- Sebuah pohon biner hampir lengkap (almost complete binary tree) adalah sebuah pohon diaman setiap simpul yang mempunyai anak kanan juga memiliki anak kiri. Memiliki anak kiri tidak memerlukan sebuah simpul untuk mempunyai anak kanan. Penjelasan lainnya, sebuah pohon biner hampir lengkap adalah sebuah pohon dimana untuk sebuah anak kanan, selalu terdapat anak kiri, tetapi untuk sebuah anak kiri, tidak selalu terdapat sebuah anak kanan.
- Jumlah simpul n dalam pohon biner lengkap dapat dihitung dengan menggunakan rumus: n = 2^(h+1)-1 dimana h adalah tinggi dari pohon.
- Jumlah daun n dalam sebuah pohon biner lengkap dapat dihitung dengan menggunakan rumus: n = 2^h dimana h adalah tinggi dari pohon.
Definisi dalam teori graf
Dengan akar yang dipilih, setiap sudut akan memiliki ayah khusus, dan diatas dua anak; bagaimanapun juga, sejauh ini terdapat keterbatasan informasi untuk membedakan antara anak kiri atau kanan. Jika kita membuang keperluan yg tak terkoneksi, membolehkan bermacam koneksi dalam komponen di gafik, kita memanggil struktur sebuah hutan.
Sebuah jalan lain untuk mendefinisikan pohon biner melalui definisi rekursif pada grafik langsung. Sebuah pohon biner dapat berarti:
- Sebuah sudut tunggal.
- Sebuah graf yang dibentuk dengan mengambil dua pohon biner, menambahkan sebuah sudut, dan menambahkan sebuah panah langsung dari sudut yang baru ke akar daris setiap pohon biner.
Kombinatorik
Kelompok dari sepasang simpul dalam sebuah pohon dapat digambarkan sebagai pasangan dari aksara dalam tanda kurung. Oleh sebab itu, (a,b) menunjukan pohon biner dimana sub pohon kirinya adalah a sedangkan sub pohon kanannya adalah b. Benang dari tanda kurung yang seimbang mungkin dapat digunakan untuk menunjukan pohon biner pada umumnya. Himpunan dari semua benang yang mungkin yang terdiri dari keseluruhan tanda kurung yang seimbang dikenal sebagal bahasa Dyck.
Diketahui n+1 simpul, jumlah seluruh jalan dimana simpul tersebut dapat disusun kedalam sebuah pohon biner dengan sebuah bilangan Catalan 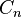 . Sebagai contoh,
. Sebagai contoh, 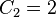 adalah pernyataan bahwa (ab)c dan a(bc) merupakan dua pohon biner yang mungkin, yang memiliki 3 simpul.
adalah pernyataan bahwa (ab)c dan a(bc) merupakan dua pohon biner yang mungkin, yang memiliki 3 simpul.
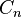 . Sebagai contoh,
. Sebagai contoh, 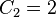 adalah pernyataan bahwa (ab)c dan a(bc) merupakan dua pohon biner yang mungkin, yang memiliki 3 simpul.
adalah pernyataan bahwa (ab)c dan a(bc) merupakan dua pohon biner yang mungkin, yang memiliki 3 simpul.
Kemampuan untuk menggambarkan pohon biner sebagai benang dari simbol-simbol dan tanda kurung secara tidak langsung menyatakan bahwa pohon biner dapat mewakili elemen dari magma. Sebaliknya, himpunan dari semua pohon biner yang mungkin, bersama-sama dengan operasi natural memasangkan pohon dari satu ke yang lain, dari sebuah magma, magma bebas.
Memberikan benang yang menggambarkan sebuah pohon biner, operator untuk mendapatkan sub pohon kiri dan kanan kadang-kadang mengacu sebagai CAR dan CDR.
Metode untuk menyimpan pohon biner
Pohon biner dapat dikonstruksi dari bahasa pemrograman primitif dalam berbagai cara. Dalam bahasa yang menggunakan records dan referensi, pohon biner secara khas dikonstruksi dengan mengambil sebuah struktur simpul pohon yang memuat beberapa data dan referensi ke anak kiri dan anak kanan. Kadang-kadang itu juga memuat sebuah referensi ke ayahnya yang khas. Jika sebuah simpul mempunyai kurang dari dua anak, beberapa penunjuk anak dapat diatur kedalam nilai nol khusus, atau ke sebuah simpul sentinel.
Pohon biner dapat juga disimpan sebagai struktur data implisit dalam array, dan jika pohon tersebut merupakan sebuah pohon biner lengkap, metode ini tidak boros tempat. Dalam penyusunan yang rapat ini, jika sebuah simpul memiliki indeks i, anaknya dapat ditemukan pada indeks ke-2i+1 dan 2i+2, meskipun ayahnya (jika ada) ditemukan pada indeks lantai((i-1)/2) (asumsikan akarnya memiliki indeks kosong). Metode ini menguntungkan dari banyak penyimpanan yang rapat dan memiliki referensi lokal yang lebih baik, tersitimewa selama sebuah preorder traversal. Bagaimanapun juga, ini terlalu mahal untuk perkembangannya dan boros tempat sebanding dengan 2h - n untuk sebuah pohon dengan tinggi h dengan nsimpul.
Dalam bahasa dengan tagged union seperti ML, sebuah simpul pohon seringkali sebuah tagged union dari dua jenis simpul, dimana yang satu merupakan data dari 3-tupel, anak kiri, dan anak kanan, dan yang lain dimana sebuah daun, yang tidak memuat data dan fungsi seperti nilai nol dalam bahasa dengan penunjuk (pointers)
Metode iterasi pohon biner
Pre-order, in-order, dan post-order traversal
Pre-order, in-order, dan post-order traversal mengunjungi setiap simpul dalam sebuah pohon dengan pengunjungan secara berulang-ulang pada sub pohon kiri dan kanan dari akarnya. Jika akarnya dikunjungi sebelum sub pohonnya, ini merupakan preoder. Jika akarnya dikunjungi sesudah sub pohonnya, ini dinamakan postorder dan jika akarnya dikunjungi di antara sub pohonnya, dinamakan inorder. In-order traversal sangat berguna dalam pohon biner terurut, dimana traversal ini mengunjungi simpul dalam urutan yang meningkat.
Depth-first order
Breadth-first order
Penyandian
Penyandian ringkas
Sebuah struktur data ringkas adalah sesuatu yang mengambil tempat minimum mutlak yang mungkin, yang berdiri sebagai teori informasi bawah. Jumlah dari pohon biner yang berbeda pada  simpul adalah
simpul adalah  , Bilangan Catalan ke-
, Bilangan Catalan ke- (asumsikan kita melihat pohon dengan struktur yang identik sebagai sebuah kesamaan). Untuk besarnya
(asumsikan kita melihat pohon dengan struktur yang identik sebagai sebuah kesamaan). Untuk besarnya  , ini berkisar kira-kira
, ini berkisar kira-kira  ; sehingga kita membutuhkan setidaknya kira-kira
; sehingga kita membutuhkan setidaknya kira-kira  bit untuk menyalinnya. Oleh sebab itu sebuah pohon biner ringkas hanya membutuhkan 2 bit setiap simpul.
bit untuk menyalinnya. Oleh sebab itu sebuah pohon biner ringkas hanya membutuhkan 2 bit setiap simpul.
 simpul adalah
simpul adalah  , Bilangan Catalan ke-
, Bilangan Catalan ke- (asumsikan kita melihat pohon dengan struktur yang identik sebagai sebuah kesamaan). Untuk besarnya
(asumsikan kita melihat pohon dengan struktur yang identik sebagai sebuah kesamaan). Untuk besarnya  , ini berkisar kira-kira
, ini berkisar kira-kira  ; sehingga kita membutuhkan setidaknya kira-kira
; sehingga kita membutuhkan setidaknya kira-kira  bit untuk menyalinnya. Oleh sebab itu sebuah pohon biner ringkas hanya membutuhkan 2 bit setiap simpul.
bit untuk menyalinnya. Oleh sebab itu sebuah pohon biner ringkas hanya membutuhkan 2 bit setiap simpul.
Salah satu penggambaran sederhana yang masih berhubungan dengan ini adalah mengunjungi simpul dari pohon dengan preoder, meletakkan "1" untuk sebuah simpul dalan dan "0" untuk sebuah daun. [1] Jika pohon ini memuat data, kita dapat menyimpanya secara serempak dalam sebuah array yang berurutan dengan preoder. Fungsi ini memenuhi:
Penyandian pohon n-er sebagai pohon biner
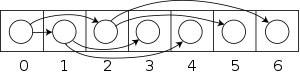
Terdapat sebuah pemetaan satu-satu antara pohon terurut general dan pohon biner, yang biasanya digunakan oleh Lisp untuk menggambarkan pohon terurut general sebagai pohon biner. Setiap simpul N dalam pohon terurut terhubung ke sebuah simpul N dalam pohon biner; anak kiri dari N merupakan simpul yang terhubung ke anak pertama dari N, dan anak kanan dari N merupakan simpul yang terhubung ke saudara selanjutnya dari N yang merupakan simpul selanjutnya dalam urutan di antara anak-anaknya dari ayahnya N
Suatu cara untuk menyelesaikan ini adalah bahwa setiap anak simpul berada dalam sebuah linked list, dihubungkan bersama dengan bidang kanan mereka, dan simpul yang hanya memiliki sebuah petunjuk ke awalnya atau kepala dari daftar ini, melalui bidang kiri nya.
Penerapan terbanyak dari pencarian biner adalah untuk mencari sebuah nilai tertentu dalam sebuah list terurut. Jika dibayangkan, pencarian biner dapat dilihat sebagai sebuah permainan tebak-tebakan, kita menebak sebuah bilangan, atau nomor tempat, dari daftar (list) nilai.
Karena pemanggilan fungsi di atas adalah rekursif ekor, fungsi tersebut dapat dituliskan sebagai sebuah pengulangan (loop), hasilnya adalah algoritma in-place:
Pencarian biner adalah sebuah algoritma logaritmik dan bekerja dalam waktu O(log n). Secara khusus, 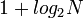 pengulangan yang diperlukan untuk menghasilkan jawaban. Hal ini dianggap lebih cepat dibandingkan sebuah pencarian linear. Pencarian biner dapat diimplementasikan dengan rekursi atau iterasi, seperti yang terlihat di atas, walaupun pada kebanyakan bahasa pemrograman akan lebih elegan bila dinyatakan secara rekursif.
pengulangan yang diperlukan untuk menghasilkan jawaban. Hal ini dianggap lebih cepat dibandingkan sebuah pencarian linear. Pencarian biner dapat diimplementasikan dengan rekursi atau iterasi, seperti yang terlihat di atas, walaupun pada kebanyakan bahasa pemrograman akan lebih elegan bila dinyatakan secara rekursif.
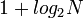 pengulangan yang diperlukan untuk menghasilkan jawaban. Hal ini dianggap lebih cepat dibandingkan sebuah pencarian linear. Pencarian biner dapat diimplementasikan dengan rekursi atau iterasi, seperti yang terlihat di atas, walaupun pada kebanyakan bahasa pemrograman akan lebih elegan bila dinyatakan secara rekursif.
pengulangan yang diperlukan untuk menghasilkan jawaban. Hal ini dianggap lebih cepat dibandingkan sebuah pencarian linear. Pencarian biner dapat diimplementasikan dengan rekursi atau iterasi, seperti yang terlihat di atas, walaupun pada kebanyakan bahasa pemrograman akan lebih elegan bila dinyatakan secara rekursif.Contoh
- Apakah angka lebih besar dari 8? (Ya)
- Apakah angka lebih besar dari 12? (Tidak)
- Apakah angka lebih besar dari 10? (Ya)
- Apakah angkat lebih besar dari 11? (Tidak)
- Apakah angka lebih besar dari 1? (Ya)
- Apakah angka lebih besar dari 2? (Ya)
- Apakah angka lebih besar dari 4? (Ya)
- Apakah angka lebih besar dari 8? (Ya)
- Apakah angka lebih besar dari 16? (Tidak, N=16, lakukan seperti di atas)
- Apakah angka lebih besar dari 12? (Tidak)
- Apakah angka lebih besar dari 10? (Ya)
- Apakah angka lebih besar dari 11? (Tidak)
Satu penerapan sederhan, pada sistem kendali revisi, dimungkinkan memanfaatkan sebuah pencarian biner untuk melihat pada revisi mana sebuah cuplikan isi ditambahkan ke sebuah file. Dengan mudah kita lakukan sebuah pencarian biner terhadap seluruh history versi; jika isi tidak ada dalam suatu versi, suatu saat kemudian pasti akan muncul, dan jika ada pasti muncul di versi tersebut atau versi berikutnya. Cara ini lebih cepat dibandingkan dengan memeriksa setiap perbedaan antar versi.
Penerapan pada teori kompleksitas
Seandainya kita tidak mengetahui sebuah jangkauan yang tetap tempat dari bilangan kberada, kita masih dapat menentukan nilainya dengan mengajukan  pertanyaan ya/tidak dalam bentuk "Apakah k lebih besar dari x?" untuk beberapa bilangan x. Sebagai konsekuensi sederhana dari cara ini, jika kita dapat menjawab pertanyaan "Apakah nilai bilangan bulat k lebih besar dari nilai yang diberikan?" pada suatu waktu kemudian kita dapat menemukan nilai dari bilangan tersebut sama lamanya ditambah dengan faktor log k. Hal ini disebut sebuah reduksi, dan karena disebabkan reduksi ini maka kebanyakan teoris kompleksitas berkonsentrasi pada permasalahan keputusan, algoritma-algoritma yang mengasihlan jawaban sederhana berupa ya/tidak.
pertanyaan ya/tidak dalam bentuk "Apakah k lebih besar dari x?" untuk beberapa bilangan x. Sebagai konsekuensi sederhana dari cara ini, jika kita dapat menjawab pertanyaan "Apakah nilai bilangan bulat k lebih besar dari nilai yang diberikan?" pada suatu waktu kemudian kita dapat menemukan nilai dari bilangan tersebut sama lamanya ditambah dengan faktor log k. Hal ini disebut sebuah reduksi, dan karena disebabkan reduksi ini maka kebanyakan teoris kompleksitas berkonsentrasi pada permasalahan keputusan, algoritma-algoritma yang mengasihlan jawaban sederhana berupa ya/tidak.
 pertanyaan ya/tidak dalam bentuk "Apakah k lebih besar dari x?" untuk beberapa bilangan x. Sebagai konsekuensi sederhana dari cara ini, jika kita dapat menjawab pertanyaan "Apakah nilai bilangan bulat k lebih besar dari nilai yang diberikan?" pada suatu waktu kemudian kita dapat menemukan nilai dari bilangan tersebut sama lamanya ditambah dengan faktor log k. Hal ini disebut sebuah reduksi, dan karena disebabkan reduksi ini maka kebanyakan teoris kompleksitas berkonsentrasi pada permasalahan keputusan, algoritma-algoritma yang mengasihlan jawaban sederhana berupa ya/tidak.
pertanyaan ya/tidak dalam bentuk "Apakah k lebih besar dari x?" untuk beberapa bilangan x. Sebagai konsekuensi sederhana dari cara ini, jika kita dapat menjawab pertanyaan "Apakah nilai bilangan bulat k lebih besar dari nilai yang diberikan?" pada suatu waktu kemudian kita dapat menemukan nilai dari bilangan tersebut sama lamanya ditambah dengan faktor log k. Hal ini disebut sebuah reduksi, dan karena disebabkan reduksi ini maka kebanyakan teoris kompleksitas berkonsentrasi pada permasalahan keputusan, algoritma-algoritma yang mengasihlan jawaban sederhana berupa ya/tidak.
Sebagai contoh, anggap kita dapat menjawab "Apakah matriks n x n ini memiliki determinan lebih besar dari k?" dalam waktu O(n2). Kemudian, dengan memanfaatkan pencarian biner, kita dapat menemukan (batas atas) determinan tersebut dalam waktu O(n2log d), dimana d adalah determinan; sebagai catatan, d bukanlah ukuran dari masukan tetapi ukuran dari keluaran.
Jika terdapat himpunan A dan himpunan B (A bisa sama dengan B), maka relasi R dari A ke B adalah subhimpunan dari A×B.
Relasi dan fungsi proposisi
Sebuah relasi dapat dikaitkan dengan sebuah fungsi proposisi atau kalimat terbuka yang himpunan penyelesaiannya tidak lain adalah relasi tersebut.
Relasi A×A
Relasi Refleksif
Relasi Irefleksif
Relasi Simetrik
Relasi Anti-simetrik
Relasi Transitif
Relasi khusus
Relasi Ekivalen
Relasi ekuivalen memiliki hubungan erat dengan partisi, yang merupakan alasan mengapa partisi dari sebuah himpunan disebut kelas ekivalen atau kelas kesetaraan.
 Orde Parsial
Orde Parsial
Didalam dunia komputer kita mengenal empat jenis bilangan, yaitu bilang biner, oktal, desimal dan hexadesimal. Bilangan biner atau binary digit (bit) adalah bilangan yang terdiri dari 1 dan 0. Bilangan oktal terdiri dari 0,1,2,3,4,5,6 dan 7. Sedangkan bilangan desimal terdiri dari 0,1,2,3,4,5,6,7,8 dan 9. Dan bilangan hexadesimal terdiri dari 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E dan F.
| Biner | Oktal | Desimal | Hexadesimal |
|---|---|---|---|
| 0000 | 0 | 0 | 0 |
| 0001 | 1 | 1 | 1 |
| 0010 | 2 | 2 | 2 |
| 0011 | 3 | 3 | 3 |
| 0100 | 4 | 4 | 4 |
| 0101 | 5 | 5 | 5 |
| 0110 | 6 | 6 | 6 |
| 0111 | 7 | 7 | 7 |
| 1000 | 10 | 8 | 8 |
| 1001 | 11 | 9 | 9 |
| 1010 | 12 | 10 | A |
| 1011 | 13 | 11 | B |
| 1100 | 14 | 12 | C |
| 1101 | 15 | 13 | D |
| 1110 | 16 | 14 | E |
| 1111 | 17 | 15 | F |


























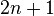 bit pada bagian akhir, dimana
bit pada bagian akhir, dimana 
 pertanyaan yang dibutuhkan untuk mendapatkan angka tersebut, karena setiap pertanyaan menghilangkan setengah dari ruang pencarian. Sebagai catatan bahwa dibutuhkan kurang dari satu pertanyaan (iterasi) untuk algoritma umum, karena angka tersebut dibatasi oleh sebuah jangkauan tertentu.
pertanyaan yang dibutuhkan untuk mendapatkan angka tersebut, karena setiap pertanyaan menghilangkan setengah dari ruang pencarian. Sebagai catatan bahwa dibutuhkan kurang dari satu pertanyaan (iterasi) untuk algoritma umum, karena angka tersebut dibatasi oleh sebuah jangkauan tertentu.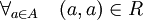




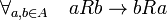
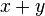 genap” adalah relasi simetrik, karena untuk sembarang x dan y yang kita pilih, jika memenuhi relasi tersebut, maka dengan menukarkan nilai y dan x, relasi tersebut tetap dipenuhi. Misalnya untuk pasangan (5, 3) relasi tersebut dipenuhi, dan untuk (3, 5) juga.
genap” adalah relasi simetrik, karena untuk sembarang x dan y yang kita pilih, jika memenuhi relasi tersebut, maka dengan menukarkan nilai y dan x, relasi tersebut tetap dipenuhi. Misalnya untuk pasangan (5, 3) relasi tersebut dipenuhi, dan untuk (3, 5) juga.



 bersifat anti-simetrik, karena
bersifat anti-simetrik, karena  mengakibatkan
mengakibatkan  . Demikian juga jika ada p dan q yang terhadap mereka berlaku
. Demikian juga jika ada p dan q yang terhadap mereka berlaku  dan
dan 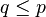 berarti
berarti 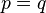 .
.

